アイパターンとは，システムに信号を入力した際の応答を，重ね合わせて表示した図のことです．通常オシロスコープなどを使用して取得されるため，Web上にプログラムを用いたシミュレーションが見つかりません．

今回は，最も単純な理想ローパスフィルタに対して，インパルス信号を複数入力した場合のアイパターンをPython3で書いていきます．

ついでに，ローパスフィルタがナイキストの第一基準を満たすことを確認し，どのくらいの間隔で情報を配置することが好ましいのかを確認します．

アイパターンやローパスフィルタの性質を，最も単純なインパルス信号によって確認していくことを目的としています．

対象とする方

信号処理を学び始めた方
アイパターンの原理を理解したい方
周波数と時間を行き来しているうちに頭がごっちゃになってしまう方
Pythonのシミュレーションに慣れたい方
アイパターンのシミュレーション用コードが欲しい方(末尾にColaboratoryのリンクを載せます)

Contents

0.1 書いた理由

1 手順
2 演習問題
- 2.1 1 逆フーリエ変換の練習
- 2.2 2. その他のフィルタ

書いた理由

Interface 5月号を読んだら，無線信号のシミュレーションをPython3でやっていて，Pythonでアイパターンのシミュレーションを書きたくなりました．

手順

用意するもの

Python3 (Jupyter Lab / Coraboratory などを利用すると，グラフを確認しながら進めることができます)

想定するローパスフィルタの形状

ローパスフィルタは，以下の周波数応答 \(H(\omega)\) を想定します．

\[ H(\omega) =
\begin{cases}
1 & |\omega| \lt \pi/T_0\\
0 & |\omega| \gt \pi/T_0\\
\end{cases}
\]

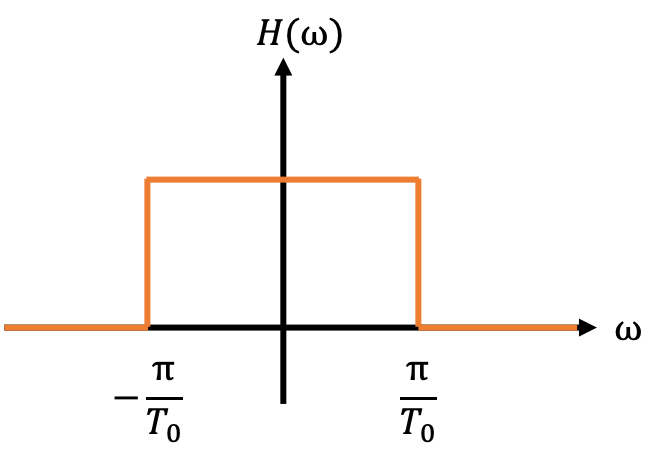
ここで，\(T_0\)はナイキスト間隔と呼ばれます．逆フーリエ変換した後にこの変数の意味がわかるので，そのタイミングで説明します．

また，0~プラス方向だけでなく，マイナス方向にもフィルタの応答を設けているのは，積分をしやすくするためです．

\(H(\omega)\) を逆フーリエ変換すると，

\[h(t) = \frac{1}{T_0} \rm{sinc}(\frac{\pi t}{T_0})\]

となります．

簡単のため，\(T_0=1\)と仮定して，\(h(t) = \rm{sinc}(\pi t) \) のグラフを描画すると以下のようになります．

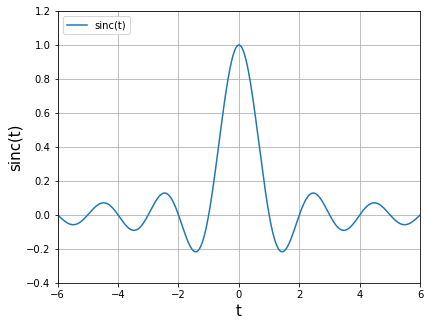
ここでは，Numpy ライブラリの sinc 関数を利用しました．\(h(t) = \rm{sinc}(\pi t) \) のうち，\(\pi\)は，積分結果を1に正規化するための値です．Numpyのsinc関数では，デフォルトで正規化が行われるため，sinc(t)の結果を表示しています．

この結果を見ると，-2, -1, 0, 1, 2 のように整数値のタイミングで0となっていることがわかります(ゼロ交差，Zero Crossing)．

つぎに，\(T_0=2\)の例を確認します．

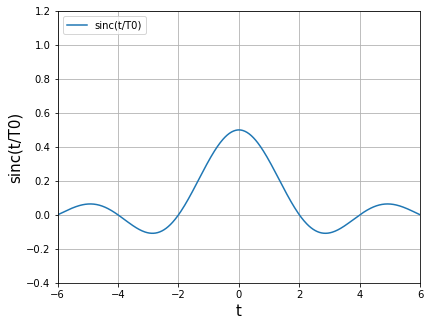
\(T_0=2\)のとき，\(t = 2z (z は整数)\)の点で，ゼロ交差しています．

帰納的に確認しましたが，ローパスフィルタを逆変換した式\( h(t) = \frac{1}{T_0} \rm{sinc}(\frac{\pi t}{T_0}) \) には，以下の性質があります．

ー　\(t = T_0 z \) (zは整数) の地点でh(t)の値はゼロとなる(ゼロ交差する)

このように，「あるフィルタの応答が，等間隔でゼロ交差する」という性質のことをナイキストの第一基準といい，その間隔\(T_0\)をナイキスト間隔といいます．

これより後は，簡単のために，\(T_0=1\) と固定して話を進めることにします．

ここまでの話で，フィルタへの入出力を時間軸で確認します．一言で言えば，インパルス信号をローパスフィルタに入れたら，下図右側のOutput waveが出てくるということです．

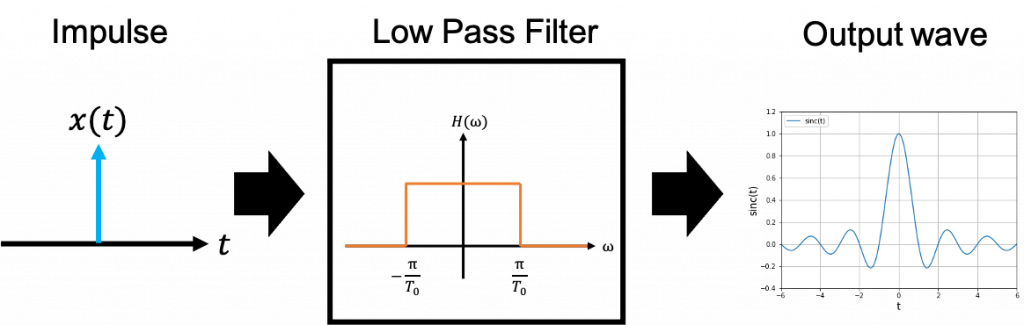
Ouput waveに示すように，応答波形には送りたい情報(右図のt=0地点)以外にも波が含まれてしまっています．

2つ以上のインパルス信号を送りたいとき，1つめのOutput waveが収まるまで待つ必要があるでしょうか？（sinc信号は厳密には\(|t|\)を増やして見ていっても，永遠に0にはなりません）1つ1つのビットを，output waveが収まるまで待っていたら，情報を送るのに膨大な時間がかかってしまいます．

そこで，ナイキストの第一基準の性質をうまく使って，インパルス信号を並べることを考えます．ナイキストの第一基準を満たすフィルタの応答は，\(T_0\)間隔でゼロ交差します．ゼロ交差する地点に次のインパルス信号を置くことで，Low pass filterの余分な応答に影響を受けず情報を送れるのではないかというアイディアを利用します．

実際にシミュレーションで確認します．今，2進数のbit列があるとき，

\[ x(t=0) =
\begin{cases}
a & \rm{bit = 1}\\
-a &\rm{bit = 0}\\
\end{cases}
\]
\[x(t \ne 0) = 0\]

の振幅を持つインパルス信号を送るものとします．\(T_0=1\)としていますので，このインパルス信号を\(t=1\)間隔で処理する様子をシミュレーションします．インパルス信号は5つ分送ることにします(00000~11111まで32通り)．簡単のために，\(a=1\)とします．

以下は，1つずつのインパルス信号の応答を，色を変えて表示しています．11001の情報を送る場合を示します．

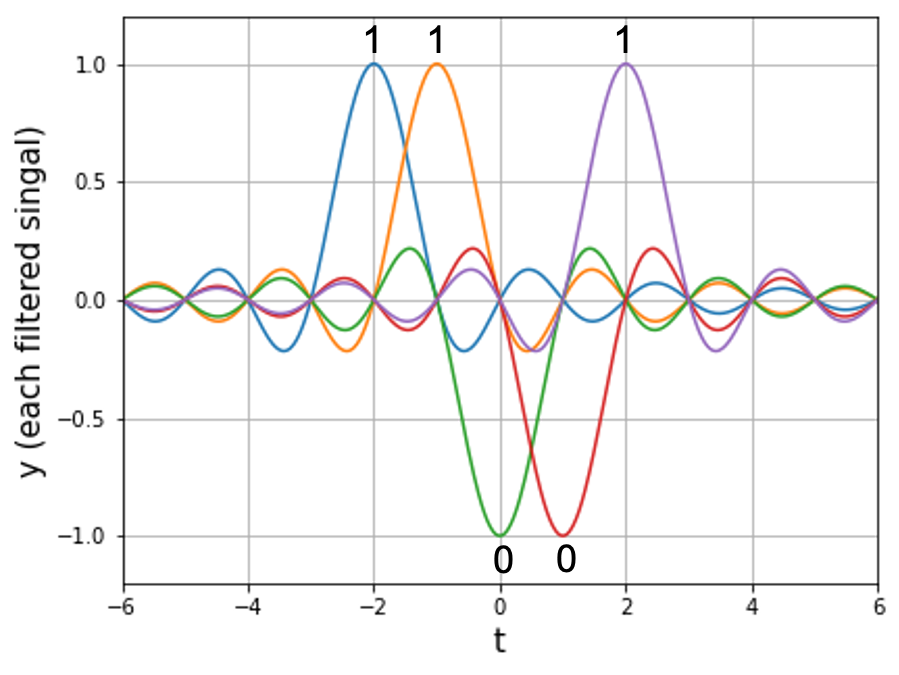
すべての信号が，同じところでゼロ交差しているのがわかります．これを足し合わせた結果が，実際にローパスフィルタから得られる信号なので，すべて足し合わせた信号を以下に示します．

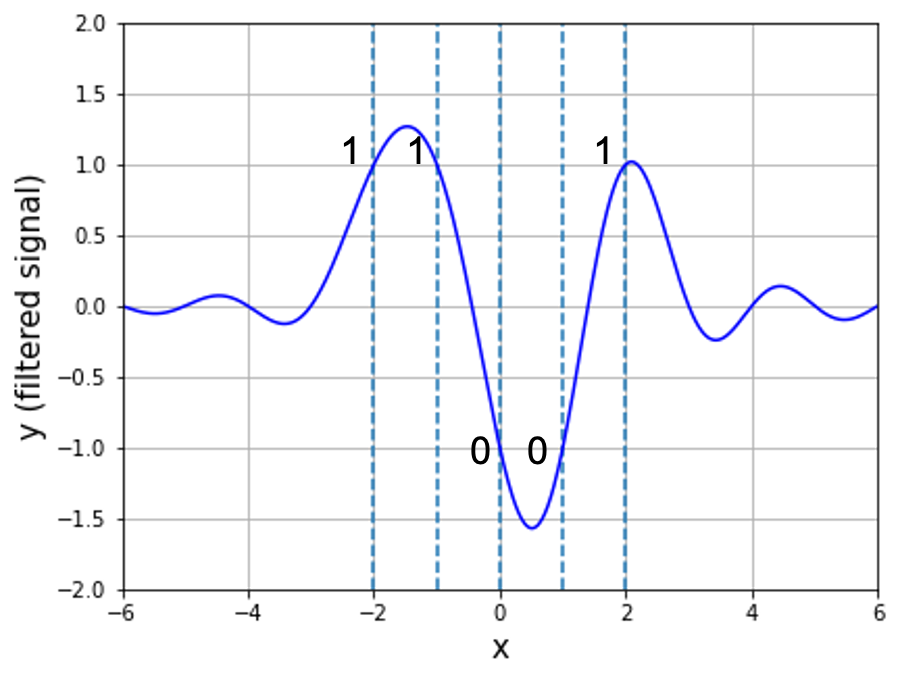
すべて足し合わせると，波はぐちゃぐちゃになったように見えますが，点線部分（情報を置いたところ）の値を確認すると，元の値を保てているのがわかります．これは，ナイキストの第一基準を満たすようなフィルタを使ったためです．いちいちフィルタの応答の波が収まるのを待たなくても，\(T_0\)の間隔を保って高速に情報を送れるようになります．

上記の作業の流れを示したものが以下になります．

上のシミュレーションでは，11001の場合を示していますが，アイパターンのシミュレーションでは，これを00000-11111 まで全通り重ねることで描画していきます．Bit全探索のアイディアを使って，32種類の応答を重ねると，

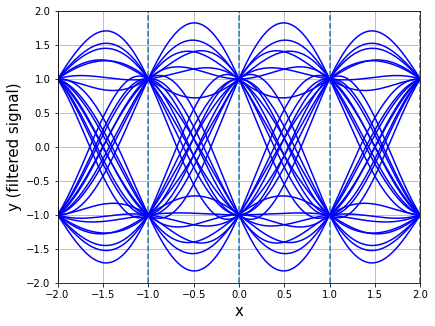
理想的なアイパターンのシミュレーションが作れました．00000-11111のどの信号においても，信号を乗せた部分（点線）は周波数応答の波の影響を受けず，1か-1どちらかに交わっているのがわかると思います．

アイパターンは目の形に似ているということで名前が付いたそうですが，どちらかというと筋肉みたいだなと思っています．

最終的なコードは以下のようになりました．

import numpy as np
import matplotlib.pyplot as plt

# グラフ用の準備
fig = plt.figure(figsize=(6.5, 5))
ax = fig.add_subplot(111)
ax.grid()
ax.set_xlabel("x", fontsize=15)
ax.set_ylabel("y (filtered signal)", fontsize=15)
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)

# 信号が残っているかの確認
for  i in range(5):
    ax.axvline(x=i-2, linestyle = "dashed")
    
    
def make_filtered_signal(message):
    # 区間[-6,6]を512分割
    t = np.linspace(-6, 6, 512)
    # 出力用の配列
    y = np.zeros(512) 
    
    for m in range(5):
        if (message & (1 << m)): 
            a = 1
        else:
            a = -1
        
        sc = a * np.sinc(t-(m-2))
        y += sc
    return y

for message in range(0, 31):

    y = make_filtered_signal(message)
    ax.plot(t, y, color = "blue")
    

# 凡例を表示
# ax.legend(loc="upper left")

# 画像を保存
plt.savefig("filtered-signal-sum.png", bbox_inches = "tight")

END

コード一覧はColaboratoryに載せてます．https://colab.research.google.com/drive/1XwxGLL_TwxRN6UVdRGgUAaUMcZSSuA50?usp=sharing

参考文献

演習問題

1 逆フーリエ変換の練習

\[ H(\omega) =
\begin{cases}
1 & |\omega| \lt \pi/T_0\\
0 & |\omega| \gt \pi/T_0\\
\end{cases}
\]

を逆フーリエ変換した際に，

\[h(t) = \frac{1}{T_0} \rm{sinc}(\frac{\pi t}{T_0})\]

となることを示してください．

2. その他のフィルタ

\(h(t)\)を，ローパスフィルタ以外の応答に変更して，アイパターンを生成してみてください．ローパスフィルタと比べてどのような違いがあるでしょうか？