Contents
はじめに
Obsidian とは,知的生産に特化したナレッジベースアプリケーション (メモ管理アプリ)の一種です.ドキュメントはすべてMarkdownで作成することができ,Notionなどのほかのナレッジベースと同様に,項目間にリンクをはることができます.
Obsidianの特徴として,リンクをはった項目間を可視化することができるグラフビューという機能があります.この機能のおかげで,「思考の整理学」「TAKE NOTES」などの書籍で紹介されているような,カードを使ってつなぎ合わせる知的生産術のデジタル版として使えるといわれてます.
とくに,TAKE NOTESの本で紹介されている,「Zettlelkasten(ツェッテルカステン)」という知的生産のためのメモ術は,生涯で58冊の本と,数百本の記事を発表したルーマン(もと在野研究者)が開発したもので,その膨大な生産力を生み出したきっかけとして注目されています.Zettelkastenを無料のアプリで試すならObsidianがよい,という声も海外では多いようです.
私自身も論文のテーマをいろいろ考えるうえで,このようなメモ術を身に着けたいと思い,ObsidianをインストールしてZettelkastenを試しているところです.その中で,項目間にリンクをはる機能は,数学の証明の関連性等を整理するのにも使えるのではないかと思い立ち,この記事を書いてみることにしました.
今回まとめる内容は,すうがくぶんか さんの主催されていた数学ゼミのうち,「ゼミに慣れながら数学を楽しむゼミ」に参加した内容で,以下の本を読んだ内容をまとめてみています.
Obsidian の特徴的な機能に触れながら,定義や定理間のつながりを可視化して,それらがつながっていく楽しさを感じるきっかけにできないかというモチベーションでまとめます.
Obsidian を数学に使うための準備
テンプレートの作成
ページごとに最低限まとめるのにあるとよい機能を,テンプレートにまとめておき,新しい定義や定理を記入する前にテンプレートを反映してから書きまじめます.テンプレートの例を以下に示します.
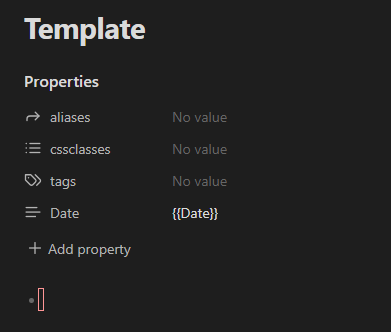
Properties から始まる一覧は,フロントマターといい,ノートに関する情報を記入していくものです.この内容のうち,aliases は,複数ある呼び方のものを,1つのノートに紐づけるためのオプションです.
例えば,「定理1-5より」と参照されることもあれば,「割り算の定理より」と参照されることもあるような場合に以下のように設定しています.
このように設定することで,以下のように,「割り算の定理」というリンクの上にポインタを持ってくると,「定理1-5」の内容がプレビューされるようになります.
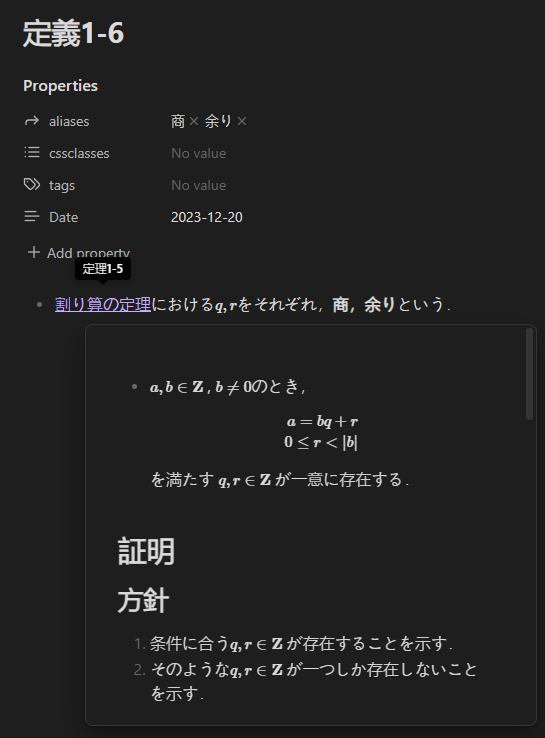
数式の書き方
Obsidianでは,文中の数式は $で囲むことによって, 1列で表現する数式は $$ で囲むことによってLaTeXの書式をつかって数式の記述が可能です.特にプラグインを入れなくても,このあたりの記述は最初からデフォルトで使えました.Obsidianは,デフォルト設定では,リアルタイムプレビューといって,編集する箇所以外はプレビューモードのように,編集する箇所は編集モードとして表示されます.
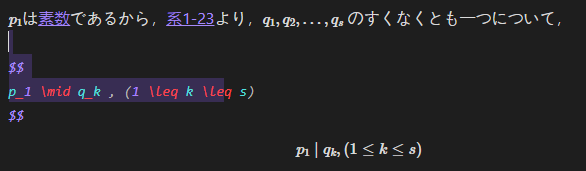
Obsidian でゼミ内容のまとめ
ここからは,すうがくぶんか さん主催の「ゼミに慣れながら数学を楽しむゼミ」に参加した内容をまとめていきます.
ゼミに参加したきっかけ
単純に趣味として数学を学びなおしたいという気持ちがあったのと,今年度から所属が変わり,暗号関連の研究に対してもコメントを求められることが増えたため,暗号に必要な数学を学びなおしたいと思い,ちょうど整数論に関するゼミが立ち上がっていたため,参加しました.
ゼミならではの理解
独学ですすめるということもできるかもしれませんが,ゼミに参加すると,思い違いなどをしたまま先に進んでしまうリスクを減らすことができます.
私の場合,商・あまりの一意性の証明のうち,以下の部分は,頭の中で暗黙に\(q’ \neq q”, r’ \neq r”\)を補って読んでおり,背理法であると思って読み進めていました.括弧書きにもあるように,これが厳密には背理法ではないということを教えていただき,さらに深い理解ができたように思います.

全体像
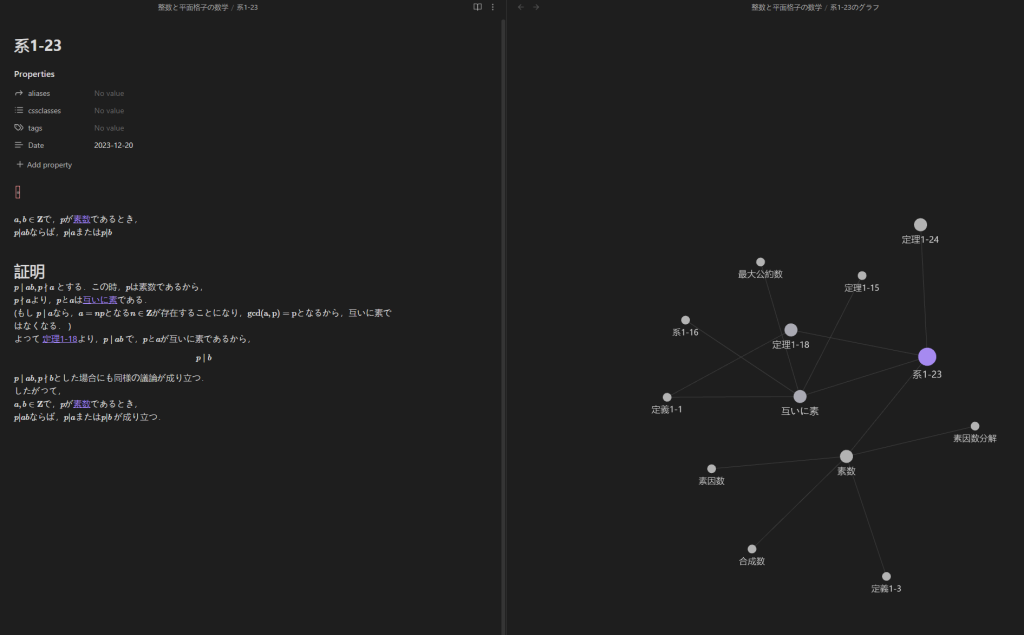
ゼミに参加してから2か月ほどが経過していますが,その内容をすべてObsidianでまとめてグラフビューで表示した結果が以下の図です.下のつながっていない一部はほかの本の学習内容で,基本的に上側の項目(ゼミで学んだ内容)はすべてつながりあっていることがわかります.
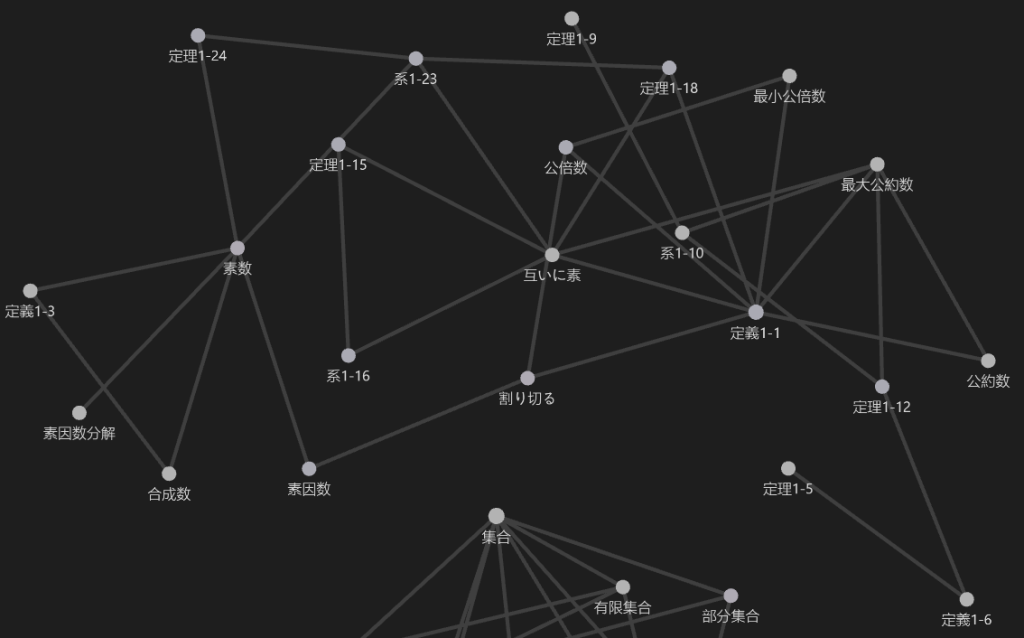
例えば,このグラフ中で系1-23をクリックすると,以下のように直接関連する項目が色付けされて表示されます.内容の詳細は後で説明します.
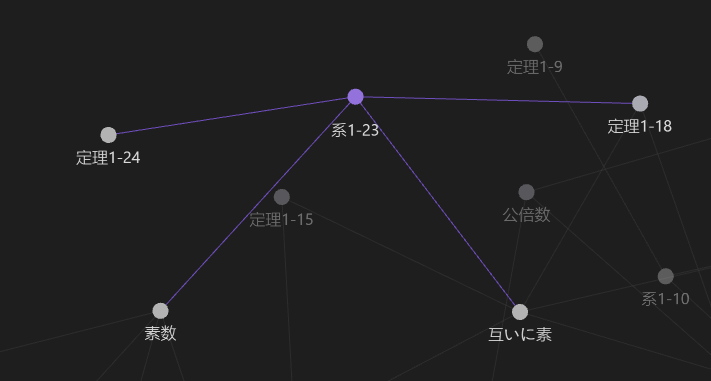
ドキュメント内で,既存の学習内容と結びつく内容のうち,最初に現れるものにのみリンクをはっていきました.例えば,[定理1-23より]と2回現れる場合には,最初の定理1-23にのみリンクをはっています.すべての既出単語にリンクをはっていくのが骨の折れる作業だからです.
リンクをはっていった様子をアニメーションとして示すことができます (最初にほかの本をまとめて中断した分が現れますが気にしないでください).
つながりを実感できる定理の例
私自身は計算関連よりも,証明によって,今までやった定義や定理がつながっていくことが面白いと感じるので,そのあたりが実感しやすい部分についてObsidianのまとめを参照しながら説明していきます.
定理1-12 (ユークリッドの互除法が有限回で終了することの証明)
定理1-12は,以下のようになっています.
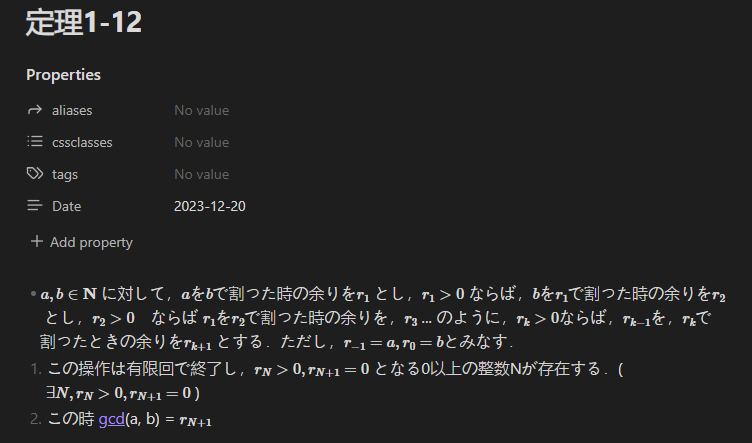
その下に,定理が何を表しているか簡単に書いて,証明を書いていきます (長いので一部たたんでいます).

また,定理1-12に関するグラフを出力すると以下のようになります.以下は,ローカルグラフといって,今閲覧しているノートとつながる頂点のみ表示しています (深さは設定から変更でき,図では深さは2に設定).
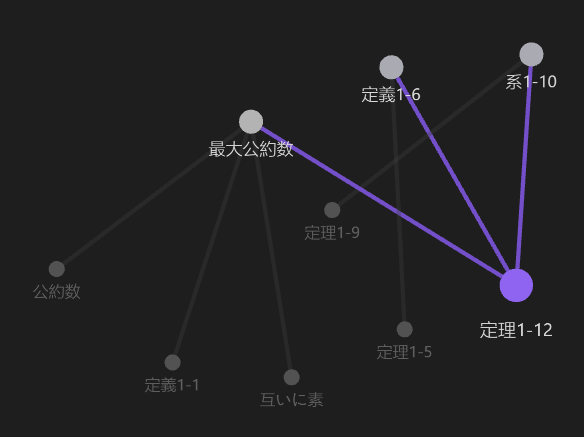
直接関係のあるものは,証明のリンク部分と,グラフの紫で示されたところを見ると,「最大公約数の定義」「余りの定義(定義1-6)」「ユークリッドの互除法 (系1-10)」であることが可視化されます.
数学のゼミや,数学書を厳密に読むことに慣れていない場合,証明をただ読んでいるだけでは,なんとなく既出の定義や定理を読み飛ばしてしまう場合もあるかと思います.Obsidianでまとめた場合,リンクがはられているところについて,いったん立ち止まって,ポインターを合わせる前に,「定義であれば,内容を詳細に把握しているか?覚えているか?」「定理であれば,それが成り立つ条件も込みで理解しているか?」を自分の頭の中で考えながら読むことができます (前の項目の理解確認の役割を果たせる).
定理1-24 2以上の任意の整数について,素因数分解が一意にできることの証明.
次に,素因数分解の一意性について述べている,定理1-24について取り上げます.
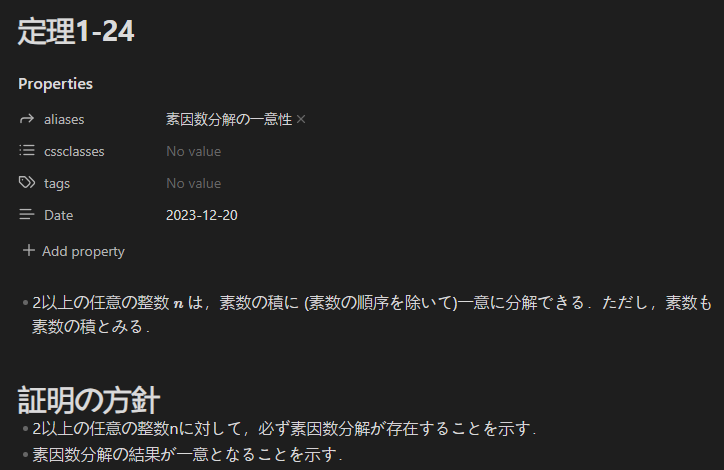
定理の内容と証明の方針は以下の通りです.

以下はそれに伴って生成されたローカルグラフです.
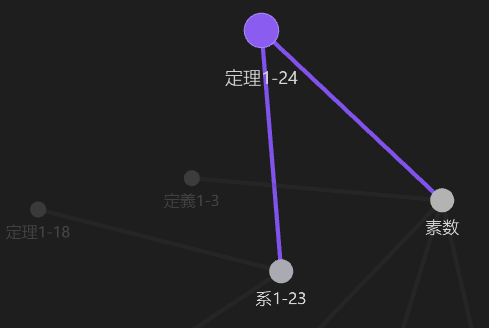
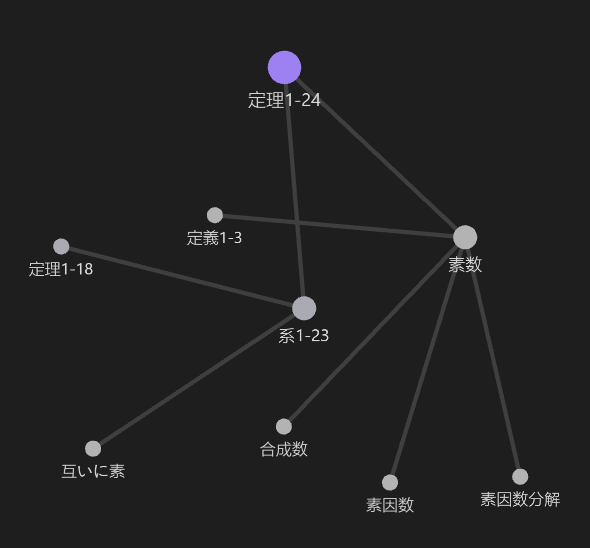
定理 1-24の証明のためには,系1-23 と素数しか使わない単純な構造に見えるかもしれませんが,系1-23を証明するためには定理1-18が必要,定理1-18を証明するためには\(b\mid a\)の定義を理解している必要があります.
順を追って,接続されている定理や系を確認していきます.
以下は,系1-23の内容とグラフです.
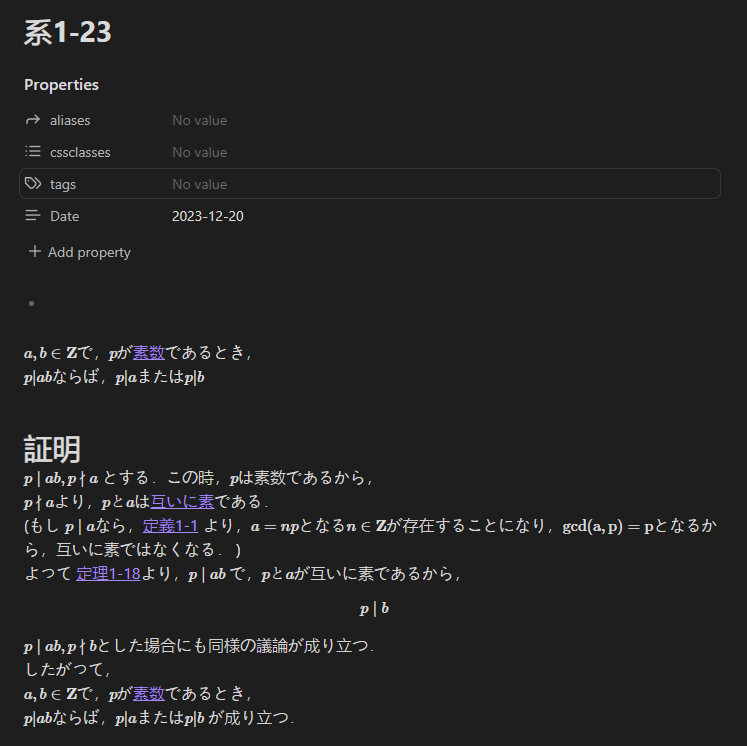
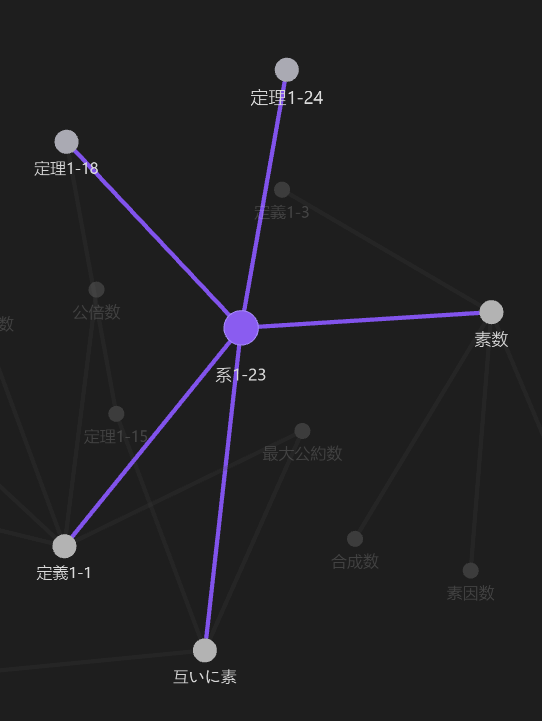
ここで,証明の部分で,なぜ \(p\)が素数で,\(p \mid a\)でない ならば,\(p とa\)が互いに素なのかについて括弧書きで説明を追記していますが,この説明をするためには,定義1-1の「割り切る」「割り切れる」「\(b \mid a\)」の定義が定着していると,自力で理由に納得できることになります.最後に,定理1-18についてみていきます.

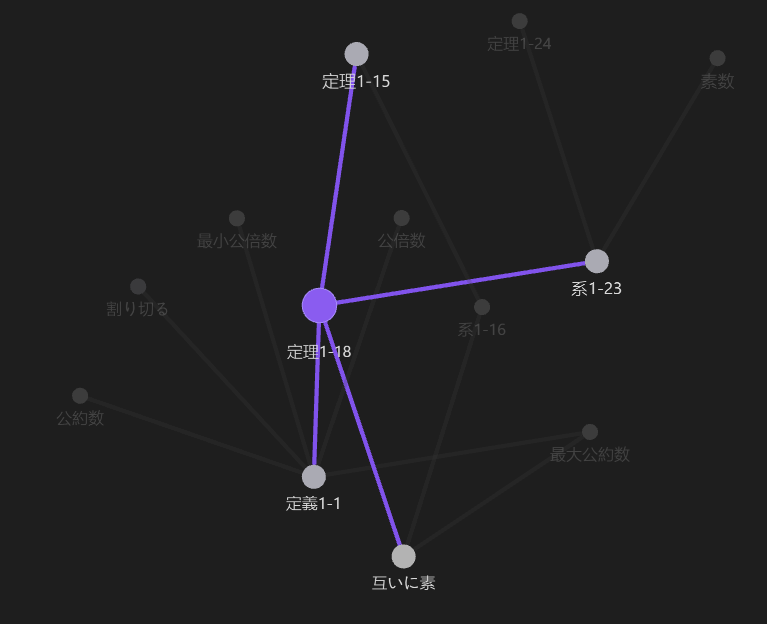
定理1-18を証明するためには,定理1-15[ \(a, b \in \mathbf Z, \rm{gcd}(a, b) = 1\)のとき,\(ax + by = 1を満たすx, y \in \mathbf Z\)が存在する] と,互いに素の定義,定義1-1のうち \(b | a\)を理解していることが必要です.例えば,さらっと 「両辺に \(b\)をかけると」fと書かれていますが,これは,\(n | b\) の定義が,\(n(何らかの整数) = b\)で表せることから生まれる発想で,適当に読んでいると見過ごしてしまいます.
また,定理1-18に最初に触れた際には,何のためにこの定理を証明する必要があるのか?というのがいまいちわからなかったところがありましたが,これは素因数分解の一意性のために必要な,定理1-23 [\(a, b \in \mathbf Z\)で,\(p\)が素数であるとき,\(p \mid ab ならば,p \mid a または p \mid b\) ] を証明するために必要だったのか,という理解につながります.振り返りの際に,どういう関係性だったのかがわかりやすくなるという役割があります.
定理1-15以上は省略しますが,このように,学んだ定義や定理がつながっていくところは久しぶりに数学に触れてみても面白いと思いました (はじめは身近にいる文系出身の方に,どこがおもしろいのかと聞かれて説明しようと思って作っていました).
数学を学ぶ上でのおすすめの使い方 (個人的な感想)
今回は,ゼミに参加する際には本を読みながらノートにまとめ,Obsidianにまとめる際には,なるべくノートを見ずにまとめようとして,思いつかないところをノートにチェックしつつ,まとめていきました.いきなり電子ツールにまとめると,なんとなく読んで書き写すだけになってしまうこともあると思うので,学んだ内容の再整理という位置付けで,関連性を復習するような形でまとめていくのがいいのではないかと思います.
教育に携わる人の場合には,中学数学の証明パートにあたる 三角形の合同 の説明の部分で,生徒に実際に作ってもらう,または先生が前でグラフを見せながら説明するといった使い方もできるのではないかと思います.
おわりに
今回は,
- リンクの作成によって,証明そのものを読んでいるときに,過去に学んだ定義や定理の理解度確認を[スムーズに行うのに or 意識的に行うのに]役立つのではないか?(テストやゼミなどで本なしで説明することが求められている場合など)
- グラフ表示やアニメーションの活用によって,学んだ数学の内容を育てているような感覚が得られるのではないか?
- 証明が苦手な学生・生徒に,つながっていく感覚の面白さを知ってもらうための教育ツールとして使えないか?
などの観点で,Obsidianによって,学んだ内容をまとめてみました.大人になると,定期テストのようなものを課されることがなく,ゼミに一回参加して発表した/聞いただけではどういうことだったか忘れてしまうということもあると思うので,このようなツールを確認テスト代わりに利用していきたいと思います.ゼミのタイトル「ゼミに慣れながら数学を楽しむゼミ」の通り,このような関連性を楽しみながらひきつづき勉強していきたいと思います.
最後まで読んでくださりありがとうございました.