FFT (Fast Fourier Transform) を適用した波形をグラフとして表示するためには,得られた結果に絶対値を適用する・周波数分解能 \(\Delta f\) で割るなど,追加の処理が必要です.どのように単位を扱うのか,どのような処理を行った結果が適切なのか etc……を迷ってしまうため,各スペクトルの定義と,その単位,使いどころを簡単にメモしておくことにしました.
対象とする読者
- FFTしたデジタル波形の扱いに困っている方
- スペクトルの違いや定義がごっちゃになる方
- 振幅スペクトルを N/2 で割る理由が気になっている方 (ほかの説明の中で見かける処理)
- 以下の議論は,離散時間信号 \(x[t]\) を想定した説明です.
Contents
- 1 定義
- 1.1 説明
- 1.1.1 高速フーリエ変換 (FFT, Fast Fourier Transform) \( X[f] \)
- 1.1.2 振幅スペクトル (AS, Amplitude Spectrum) \( |X[f]| \)
- 1.1.3 パワースペクトル (PS, Power Spectrum) \( |X[f]| ^2 \)
- 1.1.4 パワースペクトル密度 (PSD, Power Spectrum Density) \( \frac{|X[f]| ^2}{ (\Delta f)} \)
- 1.1.5 振幅スペクトル密度 (ASD, Amplitude Spectrum Density) \(\sqrt{PSD}\)
- 1.1 説明
- 2 プログラムによる出力 + 確認
- 3 よくある説明: 「振幅スペクトル を(N/2)で割る」について
- 4 参考文献
定義
はじめに,FFT後の代表的な処理と,その定義,単位を表形式で示します.
| 用語 | 数式 (定義) | 単位 |
| 元信号 | \( x[t] \) | \( V \): 使いたい時間波形の縦軸の単位に合わせる |
| 高速フーリエ変換 (FFT, Fast Fourier Transform) | \( X[f] \) | – 複素数のため単位なし |
| 振幅スペクトル (AS, Amplitude Spectrum) | \( |X[f]| \) | \( V \): 元信号と同じ次元 |
| パワースペクトル (PS, Power Spectrum) | \( |X[f]| ^2 \) | \( V^2 \) |
| パワースペクトル密度 (PSD, Power Spectrum Density) | \( \frac{|X[f]| ^2}{ (\Delta f)} \) | \( V^2 / Hz \) |
| 振幅スペクトル密度 (ASD, Amplitude Spectrum Density) | \(\sqrt{PSD}\) | \( V / \sqrt{Hz} \) |
| パワースペクトル密度 dB表記 (PSD, Power Spectrum Density) | \( 10 \log PSD\) | \( dB / Hz \) |
説明
高速フーリエ変換 (FFT, Fast Fourier Transform) \( X[f] \)
\([0, f_s]\)の範囲で, \(\Delta f = f_s / N\) (\(f_s\)はサンプリング周波数) 間隔で周波数ごとのフーリエ変換結果を複素数で得た結果です. Nは,2のべき乗になるように決定したFFTの点数です.
振幅スペクトル (AS, Amplitude Spectrum) \( |X[f]| \)
FFTの結果に対して,絶対値を適用した結果です.単に絶対値を適用しただけの波形ですが,ブログなどの説明では,わかりやすさのために,絶対値を取った後,2/N で割った値が用いられることがあります(この値は,通常の定義とは異なります).その理由は後述します.
パワースペクトル (PS, Power Spectrum) \( |X[f]| ^2 \)
振幅スペクトルを2乗した結果です.パワーと呼ばれ,信号の強さを求めるとき,デシベル表記の計算を行うときに用いられます.
パワースペクトル密度 (PSD, Power Spectrum Density) \( \frac{|X[f]| ^2}{ (\Delta f)} \)
パワースペクトルのそれぞれのピーク \(|X[f]|^2 \)は,\(f\)の前後 \(\Delta f \) 分のパワーを足し合わせた結果と考えることができます.すると,\(\Delta f\)が大きいほど,周囲のパワーの合計値である\(X[f] \)は大きくなります.
パワースペクトル密度は,\(\Delta f\)の大きさの違いで,異なる結果が得られてしまうパワースペクトルを,\(\Delta f\) で割ることによってそろえる役割があります.例えば,サンプリング周波数\(f_s\)の異なるセンサから得られた信号同士のパワースペクトルを比較したい場合などはこの処理を行います.
ここで,上の式をそのまま適用した場合の単位は\( V^2 / Hz \)ですが, デシベル表記としたい場合は,求めたPSDに,\(10 \log PSD\) として\([dB/Hz]\)に変換します.通常 \([dB/Hz]\)表記に直してから比較することが多いようです.スペクトルアナライザなどもこの単位で表示されます.
振幅スペクトル密度 (ASD, Amplitude Spectrum Density) \(\sqrt{PSD}\)
PSDによって,\(f_s\)の大きさによらない比較ができるようになりましたが,単位は\( [V^2 / Hz] \) となっており,結局のところ元の信号のスケールではどんな感じなのかが直感的にわかりづらいです.ASDは,PSDのルートをとって 単位を\( [V / \sqrt{Hz}] \) とすることで,元の時間波形の単位 \([V]\)にスケールを合わせた波形表示を行うことができます.
プログラムによる出力 + 確認
順にプログラムの実行によって得られる結果を,簡単な波形で確認してみます.
波形は,以下の条件で出力します.
from scipy.fft import rfft, rfftfreq
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
N = 64 # データ数
fs = N # サンプリング周波数 (簡単のためにNと揃えます)
n = np.arange(N) # データ長もNと揃えます
f1= 5
f2 = 3
# f1 [Hz]は振幅2,f2 [Hz]は振幅1で足し合わせてみます.
data = 2*np.sin(2*np.pi*f1*n/N) + np.sin(2*np.pi*f2*n/N)
# グラフ表示
plt.figure(figsize=(8, 4))
plt.xlabel('n')
plt.ylabel('Signal [V]')
plt.plot(data)
plt.savefig("images/signal.png")振幅スペクトル
rfft_data = rfft(data)
rfft_as = np.abs(rfft_data)
rfft_freq = rfftfreq(len(data), d=1.0/fs)
plt.plot(rfft_freq, rfft_as)
plt.xlabel("frequency [Hz]")
plt.ylabel("amplitude spectrum [V]")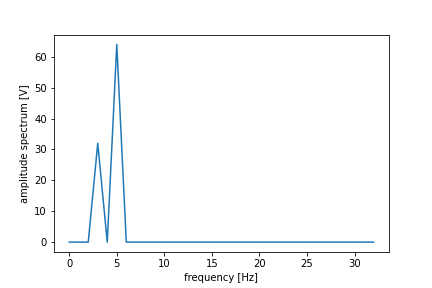
パワースペクトル
rfft_ps = pow(rfft_as, 2)
plt.plot(rfft_freq, rfft_ps)
plt.xlabel("frequency [Hz]")
plt.ylabel("power spectrum [V^2]")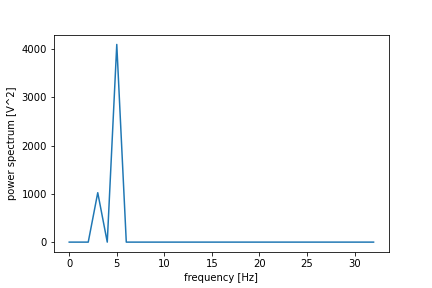
パワースペクトル密度
\(f_s = N\)としているため,違いが出ていませんが,一応載せておきます.
rfft_ps = pow(rfft_as, 2)
delta_f = fs / N
rfft_psd = rfft_ps / delta_f
plt.plot(rfft_freq, rfft_psd)
plt.xlabel("frequency [Hz]")
plt.ylabel("power spectrum density[V^2/Hz]")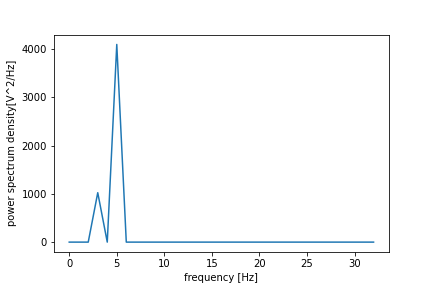
パワースペクトル密度 (dB表記)
rfft_psd_db = 10 * np.log10(rfft_psd)
plt.plot(rfft_freq, rfft_psd_db)
plt.xlabel("frequency [Hz]")
plt.ylabel("power spectrum density[dB/Hz]")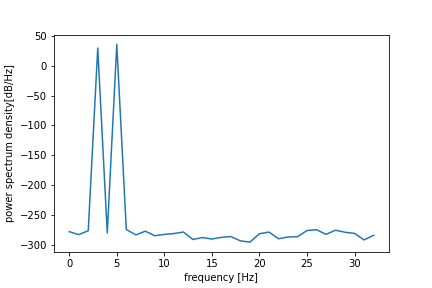
よくある説明: 「振幅スペクトル を(N/2)で割る」について
ほとんどの振幅スペクトルの求め方のブログで,「振幅スペクトル を(N/2) で割ると,整合性のとれた振幅値が得られます」(Nはデータ数,またはFFTの点数)というような説明が見られるので,どういうことか確認して,意味を考えてみました.例えば,https://teratail.com/questions/123923 などで議論がありますが,あまり数式での説明がなくわかりづらいため,まとめなおしました.
rfft_data_scaled = np.abs(rfft(data)) / (N/2)
plt.plot(rfft_freq, rfft_data_scaled)
plt.xlabel("frequency [Hz]")
plt.ylabel("amplitude spectrum (scaled by 2/N)[V]")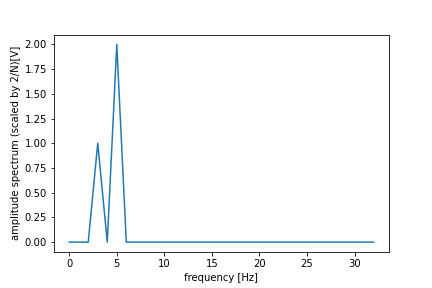
この方法で求めると,3 [Hz]のとき -> 1, 5[Hz]のとき -> 2となり,元の信号の定義と一致します.ピークの概形は変化しないため,どちらの定義の 振幅スペクトルを使ってもいいのではないかと思いますが,この理由を説明します.
離散フーリエ変換 (DFT) , 逆離散フーリエ変換 (IDFT)の定義
意味を明らかにするために,フーリエ変換とその逆変換の定義をおさらいします.
離散フーリエ変換 (DFT) の定義
\[ F[k] = \sum_{n=0}^{N-1} f[n] e^{-jw_0kn} \]
逆離散フーリエ変換 (IDFT)の定義
\[f[n] = \frac{1}{N} \sum_{k=0}^{N-1} F[k] e^{jw_0kn}\]
「振幅スペクトル を(N/2)で割る」についての解釈
ここで,逆離散フーリエ変換に着目します.この式は,「最終的に計算した結果に,\(\frac{1}{N}\)をかけないと(つまり\(N\)で割らないと ) 元の波形には戻らない」ということを意味します.
逆離散フーリエ変換の式には,FFTした結果とも読める \(F[k]\) が含まれています.
FFTした結果は,ナイキスト周波数 \(f_s/2) \) に対応する 点 \(\frac{N-1}{2} \) で,対称となっていることを考えて,逆離散フーリエ変換の式を以下のように変形します.
\[f[n] = \frac{1}{N} \sum_{k=0}^{N-1} F[k] e^{jw_0kn}\]
\[ = \frac{2}{N} \sum_{k=0}^{\frac{N-1}{2}} F[k] e^{jw_0kn}\]
\[ = \sum_{k=0}^{\frac{N-1}{2}} \frac{2}{N} F[k] e^{jw_0kn}\]
この式から,FFTした時の半分の結果(つまり0~ナイキスト周波数に対応する点 \(\frac{N-1}{2}\))のみで,元の結果を得るためには,FFTした結果それぞれに \(\frac{2}{N}\) をかける必要があります.
そのため,元の波形に対応しているような結果を,振幅スペクトルで得たい場合には,\(\frac{2}{N}\) をかける,または (\frac{N}{2}\)で割るという説明になるのだと思います (やや飛躍がありますが,その説明が一番簡単な理由になるかと思いました,参考文献 [1]を参照してください).
しかし,実際には振幅スペクトルの縦の値の厳密さというより,ピークの位置に応じた周波数(横軸)の値が欲しいことが多く,\(\frac{N}{2}\)で割るという操作をしてもピークの概形は変化しないため,ここを厳密に取り扱う必要はなさそうです(なのであまり説明が見つからないのかも).
論文やオシロスコープの会社から出ている説明を見ると, 「\(\frac{N}{2}\)で割る」を含まない振幅スペクトルの定義(最初で表で示した\( |X[f]| \))を利用しています.(実際のオシロスコープの中身がどうしているのかは不明)
もし余力があれば,続編として,実際のデータにFFTを適用した後の処理を書いていきます.(窓関数の影響を加味したFFTの結果の補正方法など)
参考文献
- Why divide the output of NumPy FFT by N?
- 小野測器 計測に関するよくある質問から -第9回- パワースペクトル密度の計算方法, 計測コラム emm 182号用
- もものきとデータ解析をはじめよう
- 伊藤 克亘 (著), 花泉 弘 (著), 小泉 悠馬 (著) Pythonで学ぶ実践画像・音声処理入門, コロナ社,2018,
- https://teratail.com/questions/123923
- Watalab, PythonでFFT実装!SciPyのフーリエ変換まとめ, 2019